Radix란 수학에서 밑(Base)를 의미하는 진법 체계에서 기준이 되는 수를 의미합니다.
예를 들어 자연수 1234가 있다면
$$ 1234 = 1 \times 10^3 + 2 \times 10^2 + 3 \times 10^1 + 4 \times 10^0 $$
으로 표현이 가능합니다.
어떤 진법을 사용해도 상관은 없지만 컴퓨터가 처리하기 좋은 이진법을 사용하여 설명을 드리겠습니다.
초기 데이터가 아래와 같을 때,
| l | e | a | r | n | a | l | g | o | r | i | t | h | m |
아래 그림은 문자를 세로로 정렬하여 이진수로 표기하여 맨 앞열은 문자를 세로로 배열한 내용이고, 7~0은 각 비트에 해당하는 이진수를 의미합니다.
최상위 비트(7bit)에서 최하위 비트(0 bit)까지 배열의 맨 앞문자('l')부터 비트 '1'인 문자를 찾고 배열의 맨 마지막 문자('m')에서 부터 역순으로 비트 '0'인 문자를 찾아 교환하는 방식(퀵정렬과 유사한 방식)으로 정렬을 합니다.
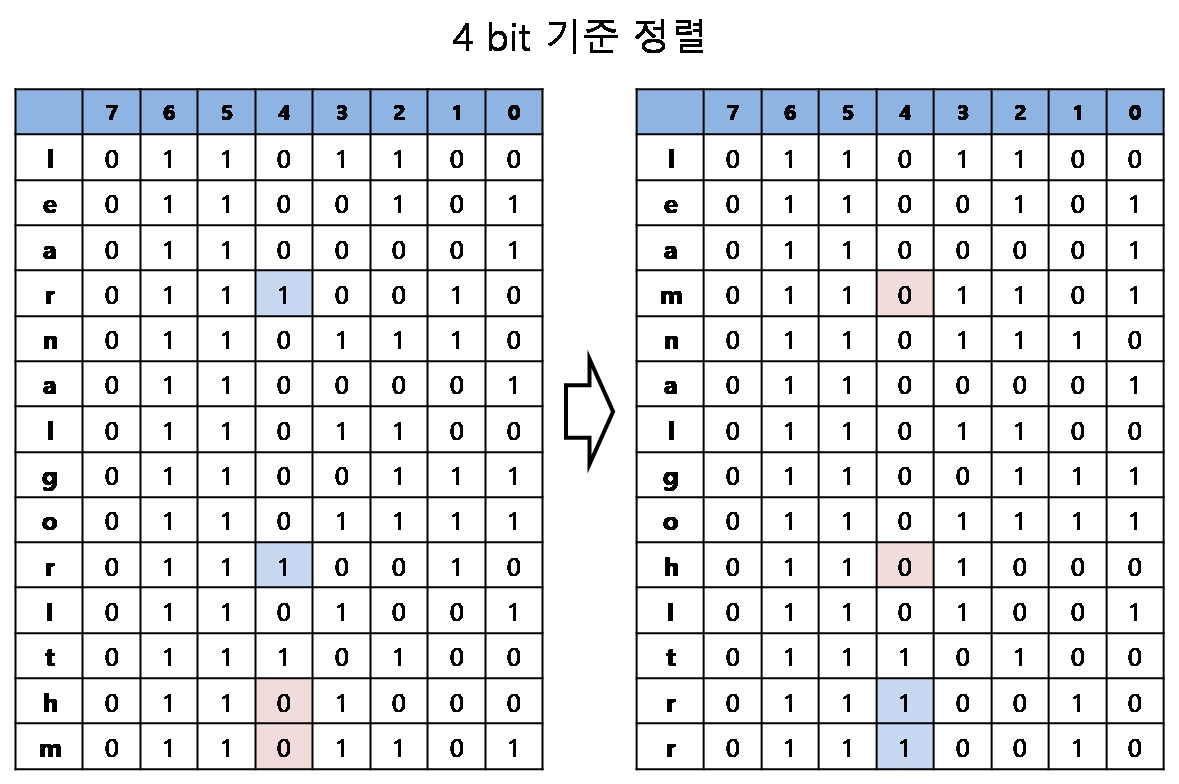
위의 예에서는 7, 6, 5비트는 모든 문자가 같은 값을 가지므로 건너뛰고, 4비트에서 보면 앞에서 부터 비트'1'인 'r'과 뒤에서 부터 비트'0'인 'm'을 교환하고, 마찬가지로 'r'과 'h'를 교환하게 됩니다. 그러면 네번째 비트까지 비교해 보면 앞에는 '0110'으로 뒤에는 '0111'인 문자로 정렬이 됩니다.
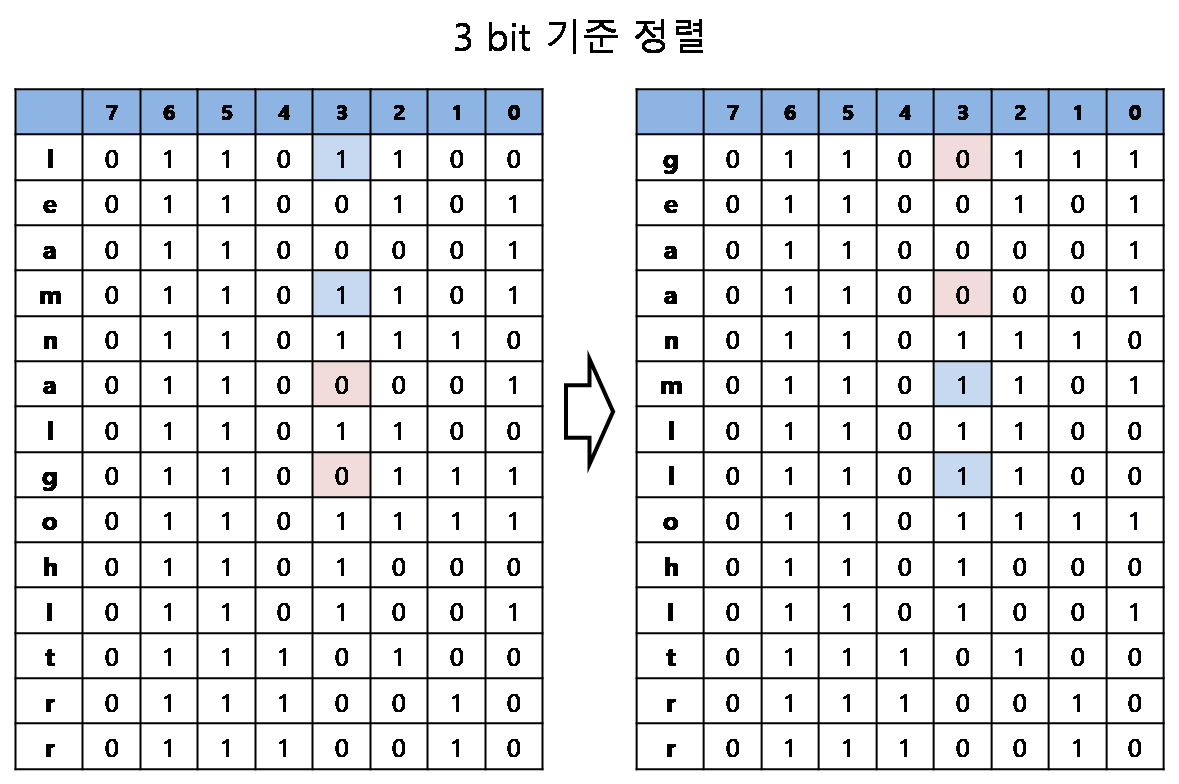
이제 3비트를 보면 'learmnalgohl'과 'trr'을 나눠서 생각할 수 있는데, 앞의 문자열을 '0'과 '1'의 순으로 교환을 하면 7~3비트까지 정렬이 됩니다. 나머지 2~0비트도 같은 방식으로 정렬을 할 수 있습니다.
다음은 C로 구현한 소스코드와 실행결과 입니다.
#include <stdio.h>
#include <string.h>
void print_data(char a[], int n);
void print_binary(char a[], int n);
char data[] = "learnalgorithm";
unsigned int bits(unsigned int x, int k, int j)
{
return (x >> k) & ~(~0 << j);
}
void radix_exchange_sort(char a[], int n, int b)
{
char t;
int i, j;
int i1, j1;
if (n > 1 && b >= 0) {
i1 = i = 0;
j1 = j = n -1;
while (1) {
while (bits(a[i], b, 1) == 0 && i < j) {
i++;
}
while (bits(a[j], b, 1) != 0 && i < j) {
j--;
}
if (i >= j) {
break;
}
printf("%d번째 비트 비교 후 교환 전 Left(%c)-Right(%c) ", b, a[i], a[j]);
print_data(data, strlen(data));
t = a[i];
a[i] = a[j];
a[j] = t;
printf("교환 후,");
print_data(data, strlen(data));
printf("\n");
/*print_data(a, n); */
}
if (bits(a[n-1], b, 1) == 0) j++;
radix_exchange_sort (a, j, b-1);
radix_exchange_sort (a+j, n-j, b-1);
}
}
void print_data(char a[], int n) {
int i;
for (i = 0; i < n; i++) {
printf ("%c ", a[i]);
}
printf ("\n");
}
void print_binary(char a[], int n) {
int i, j;
char mask;
for (i = 0; i < n; i++) {
printf ("%c(%x) : ", a[i], a[i]);
for (j = 7; j >= 0; j--) {
mask = 1 << j;
printf("%d", a[i] & mask ? 1: 0);
}
printf("\n");
}
}
void main (int argc, char *argv[])
{
print_data(data, strlen(data));
print_binary(data, strlen(data));
printf ("=======================\n");
printf ("==== 기수정렬 시작 =====\n");
printf ("=======================\n");
radix_exchange_sort(data, strlen(data), 8);
printf ("=======================\n");
printf ("==== 기수정렬 종료 =====\n");
printf ("=======================\n");
print_data(data, strlen(data));
}
PS C:\CS> .\radix_exchange.exe
l e a r n a l g o r i t h m
l(6c) : 01101100
e(65) : 01100101
a(61) : 01100001
r(72) : 01110010
n(6e) : 01101110
a(61) : 01100001
l(6c) : 01101100
g(67) : 01100111
o(6f) : 01101111
r(72) : 01110010
i(69) : 01101001
t(74) : 01110100
h(68) : 01101000
m(6d) : 01101101
=======================
==== 기수정렬 시작 =====
=======================
4번째 비트 비교 후 교환 전 Left(r)-Right(m) l e a r n a l g o r i t h m
교환 후,l e a m n a l g o r i t h r
4번째 비트 비교 후 교환 전 Left(r)-Right(h) l e a m n a l g o r i t h r
교환 후,l e a m n a l g o h i t r r
3번째 비트 비교 후 교환 전 Left(l)-Right(g) l e a m n a l g o h i t r r
교환 후,g e a m n a l l o h i t r r
3번째 비트 비교 후 교환 전 Left(m)-Right(a) g e a m n a l l o h i t r r
교환 후,g e a a n m l l o h i t r r
2번째 비트 비교 후 교환 전 Left(g)-Right(a) g e a a n m l l o h i t r r
교환 후,a e a g n m l l o h i t r r
2번째 비트 비교 후 교환 전 Left(e)-Right(a) a e a g n m l l o h i t r r
교환 후,a a e g n m l l o h i t r r
2번째 비트 비교 후 교환 전 Left(n)-Right(i) a a e g n m l l o h i t r r
교환 후,a a e g i m l l o h n t r r
2번째 비트 비교 후 교환 전 Left(m)-Right(h) a a e g i m l l o h n t r r
교환 후,a a e g i h l l o m n t r r
0번째 비트 비교 후 교환 전 Left(i)-Right(h) a a e g i h l l o m n t r r
교환 후,a a e g h i l l o m n t r r
1번째 비트 비교 후 교환 전 Left(o)-Right(m) a a e g h i l l o m n t r r
교환 후,a a e g h i l l m o n t r r
0번째 비트 비교 후 교환 전 Left(o)-Right(n) a a e g h i l l m o n t r r
교환 후,a a e g h i l l m n o t r r
2번째 비트 비교 후 교환 전 Left(t)-Right(r) a a e g h i l l m n o t r r
교환 후,a a e g h i l l m n o r r t
=======================
==== 기수정렬 종료 =====
=======================
a a e g h i l l m n o r r t기수정렬은 문자, 짧은 정수배열 등 비트수가 길지 않고, 고정된 길이의 키값을 가진 경우에만 사용할 수 있습니다. 만약 문자열을 키값으로 갖는 경우 일정 하지않은 길이와 긴 비트수로 인해 효율이 떨어질 수 밖에 없습니다.
재귀적 방법으로 구현한 위 코드는 퀵정렬과 마찬가지로 함수 호출이 많은경우 (= 데이터량이 많은 경우) 문제의 소지가 있습니다. 나중에 비재귀방법으로 구현하여 따로 포스팅하겠습니다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [C언어 알고리즘] 정렬 (8) - 병합정렬 (Merge Sort) (1) | 2020.07.21 |
|---|---|
| [C언어 알고리즘] 정렬(6) - 퀵정렬 (Quick Sort) (0) | 2020.07.13 |
| [C언어 알고리즘] 정렬(5) - 쉘정렬(Shell sort) (0) | 2020.07.11 |
| [C언어 알고리즘] 정렬(4) - 거품정렬(Bubble sort) (0) | 2020.07.09 |
| [C언어 알고리즘] 정렬(3) - 삽입정렬 (Insertion sort) (0) | 2020.07.08 |




댓글