파스칼의 삼각형은 자연수를 삼각형 모양으로 배열한 것을 말합니다.
1303년 중국인에 의해 유럽에 알려졌으나 이 삼각형에서 흥미로운 성질을 많이 발견한 프랑스의 철학자이자 수학자인 파스칼(Pascal)의 이름을 따서 파스칼의 삼각형이라 부르게 되었습니다.
파스칼의 삼각형을 잘 이용하면 여러 가지 재미있는 문제를 해결하는데 도움이 됩니다. 예를 들면, 사과와 배 두 종류만 파는 과일가게에 갔는데 과일을 사는 방법의 경우의 수를 생각해 보면 둘을 모두 사는 경우가 1가지, 둘 중 하나를 사는 경우는 사과만 살 경우와 배만 살 경우가 있으므로 2가지, 둘 다 사지 않는 경우의 수 1가지가 있습니다. 이것은 그림에서 세번 째 줄의 숫자 1, 2, 1과 같습니다. 그러면 사과, 배, 감의 세가지 과일을 사는 경우는 어떻게 될까요? 딱 봐도 감이 오죠? 고등학교에 올라가게 되면 다항식의 계수에 관한 내용을 배우는데 (이항 정리하고 합니다.) 계수의 규칙도 파스칼의 삼각형을 이용해서 알 수 있습니다.

파스칼의 삼각형으로 여러가지 규칙을 찾아 보겠습니다.
1. 파스칼의 삼각형에서 홀수를 빨간색으로 칠해보면 어떤 모양이 만들어질까요?
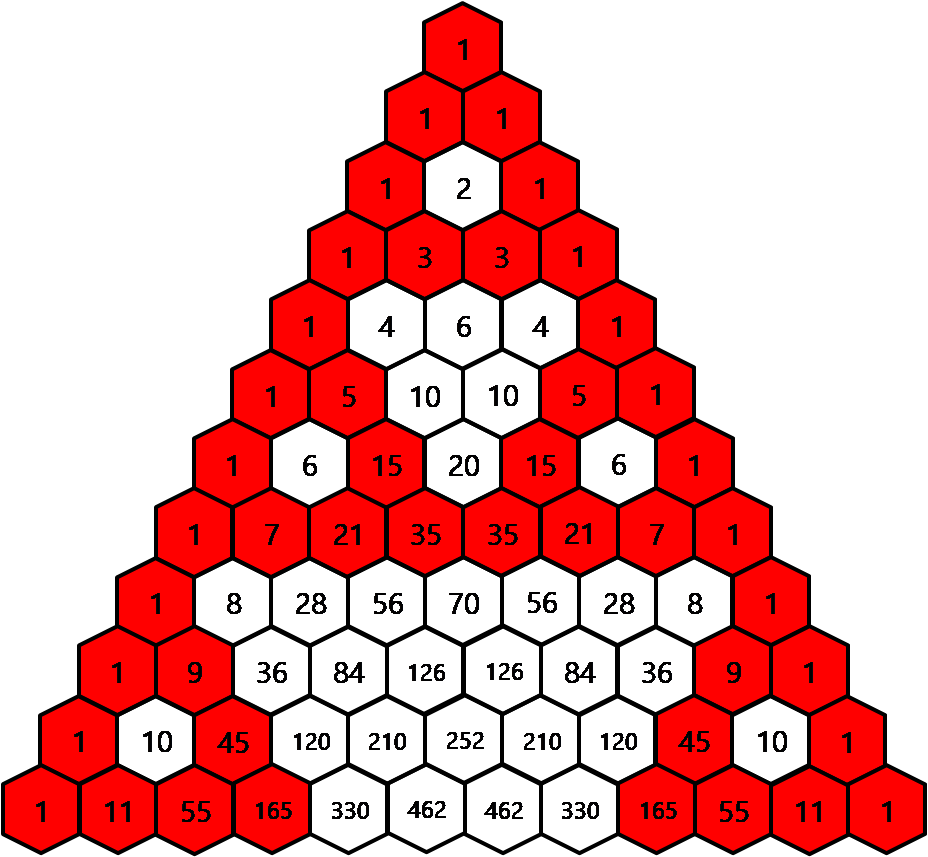
시어핀스키 삼각형은 바츠와프 시어핀스크의 이름이 붙은 프랙탈 도형으로 정삼각형의 세 중점을 연결해 내부에 정삼각형을 만드는 것을 무한히 반복하여 얻어지는 도형입니다. 고등학교에서 무한급수에 대해 배울 때 자주 등장하는 내용입니다.
2. 파스칼의 삼각형에서 5의 배수를 파란색으로 칠해보면 어떤 모양이 만들어질까요?
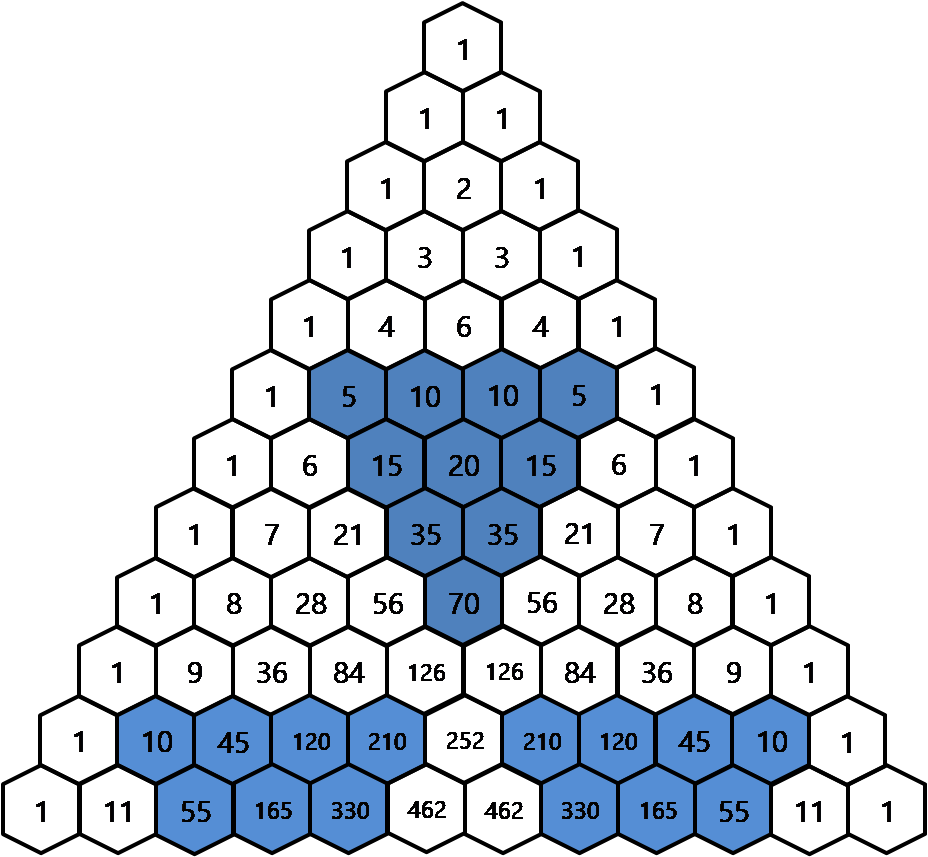
5의 배수만 색칠하게 되면 역삼각형 모양의 패턴을 찾아낼 수 있습니다.
3. 1부터 10까지의 합을 구해볼까요?
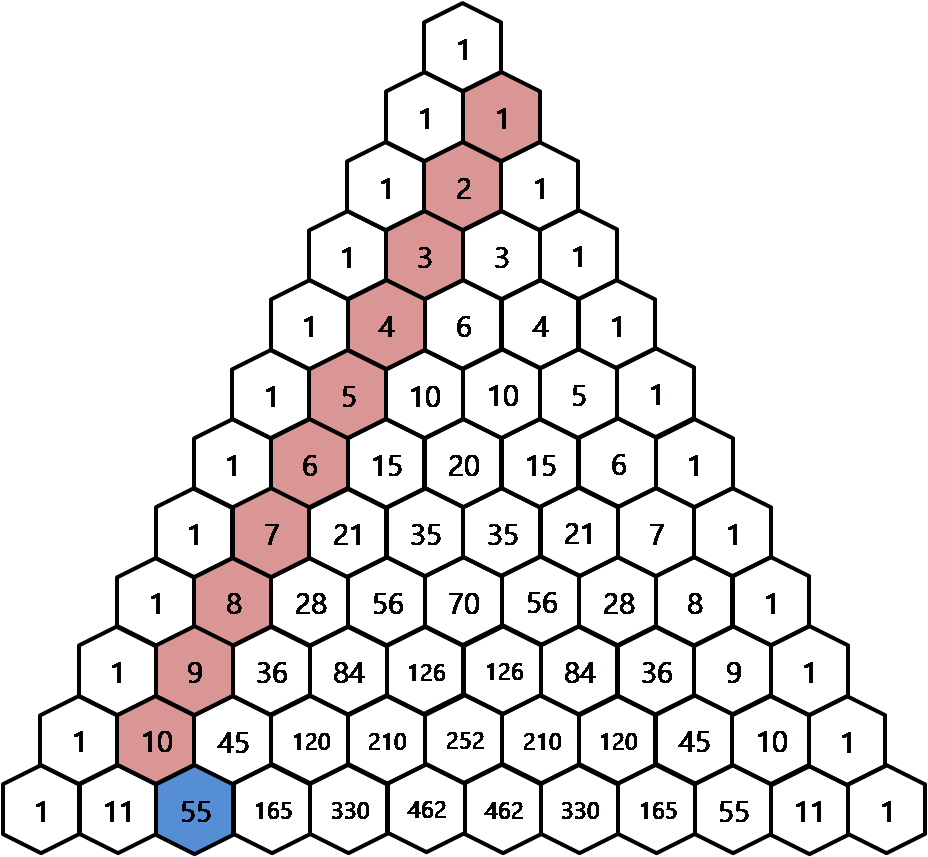
1부터 10까지의 합은 경사로를 따라 1부터 10까지 따라 내려간 후 바로 아랫 줄 꺾인 부문의 값이 더한 값이 됩니다. 위에 칠해진 바로 밑에 줄인 1, 3, 6, 10, ... 45까지 더한 값은? 당연히 165가 되겠죠? 이런 규칙을 하키스틱 법칙이라고도 한답니다.
4. 각 줄의 숫자를 더해볼까요?

각 줄을 더하면 2의 거듭제곱이라는 규칙이 있음을 알 수 있습니다.
블레즈 파스칼은 13살에 이 삼각형 모양을 발견해 이항계수를 구할 때 써먹었다고 하니 들은적은 있지만 본적은 없는 천재임이 분명합니다.
파스칼의 삼각형 활동지를 첨부합니다. 필요하신 분들은 다운로드하시길 바랍니다.
파스칼은 확률론에도 크게 기여했는데요. 당시 유명한 도박사 친구인 드메레로부터 다음과 같은 편지를 받았습니다.
“친애하는 파스칼에게, 나는 심각한 문제에 봉착했네. 실력이 비슷한 A와 B가 각각 32피스톨(화폐 단위)을 걸고 게임을 했어. 총 5판에 3판을 이기면 64피스톨을 모두 가지기로 했지. 그런데 A가 2판, B가 1판을 이긴 상황에서 일이 생겨 게임을 그만뒀어. 다시 돈을 반씩 나누면 2판이나 이긴 A가 너무 억울할 것 같고, A에게 64피스톨을 다 주면 B가 앞으로 이길 수도 있으니 공평하지 않은 듯하네. 어떻게 해야 공평할까?”
풀이는 확률을 이야기할 때 다루기로 하고, 파스칼은 자신의 풀이를 페르마에게 보냈고, 페르마는 다른 방법으로 풀어 파스칼에게 보냈다고 합니다.
'즐거운 수학 > 수학이야기' 카테고리의 다른 글
| 숫자가 2배씩 증가하면? (0) | 2020.07.28 |
|---|---|
| 나이팅게일을 아시나요? (1) | 2020.07.21 |
| 복면산 (覆面算, Verbal arithmetic) (0) | 2020.07.06 |
| 목표 수 만들기 (0) | 2020.07.05 |
| 포포즈 (Four fours) (0) | 2020.07.05 |



댓글